Reproducible El Niños

23 Feb 2016
23 Feb 2016

By Tristan Hauser

of CSAG, republished courtesy of Authorea.

A lot of attention has been given to the consequences of the latest strong El Niño event. People often often talk about meteorological phenomena as El Niño (or La Niña) conditions, but what are these, and how do we come about our notions of what is a ’typical’ El Niño event? How consistent do we expect the effects of this phenomena to be, especially when these ’signature effects’ occur thousands of kilometers away from the Pacific Ocean? Often understanding about the typical effects of large scale climate variations are derived from composites. This is a common statistical method where elements are classified into groups based on some external consideration, and then the properties of each group is expressed by the average of all the elements it contains. This can be a very efficient way to visualize large data sets, but it can also imply more consistency within groups than is actually the case. This post goes over some of mechanics of creating composites, and ways to explore to what degree they can be taken at ’face value’.


Background


Big Picture

Just briefly, what is the El Niño Souther Oscillation (ENSO)? Typically, strong winds off the coast of Equatorial South America move surface water away from the coast, which is replaced from below with cold water from the ocean depths [this colder deep water also carries nutrients which are important for sustaining marine life]. If these winds weaken, upwelling decreases, and weather patterns [as well as fish stocks] are altered by the presence of this atypically warm surface water in the Central East Pacific [1]. This is known as an El Niño event and the oscillation between El Niño and the opposing La Niña states is termed ENSO.

There are many ways that people attempt to quantify the degree to which an El Niño state is occurring. These include average sea surface temperatures over various subregions of the Pacific Ocean, differences in air pressure between different locations, and more involved metrics that combine these and other factors. An overview of the more common approaches can be found here. An El Niño event does not manifest in the same way every time it occurs, but can have many different realizations or “flavors” (Hoell 2014). Which is why, as stressed in the linked discussion, there tend to be many approaches to quantifying ENSO, each of which highlights different aspects of the variation. Looking at documented values for some of the most common indices [2] shows similar general patterns, even though the different time series have noticeably different properties.

 

 

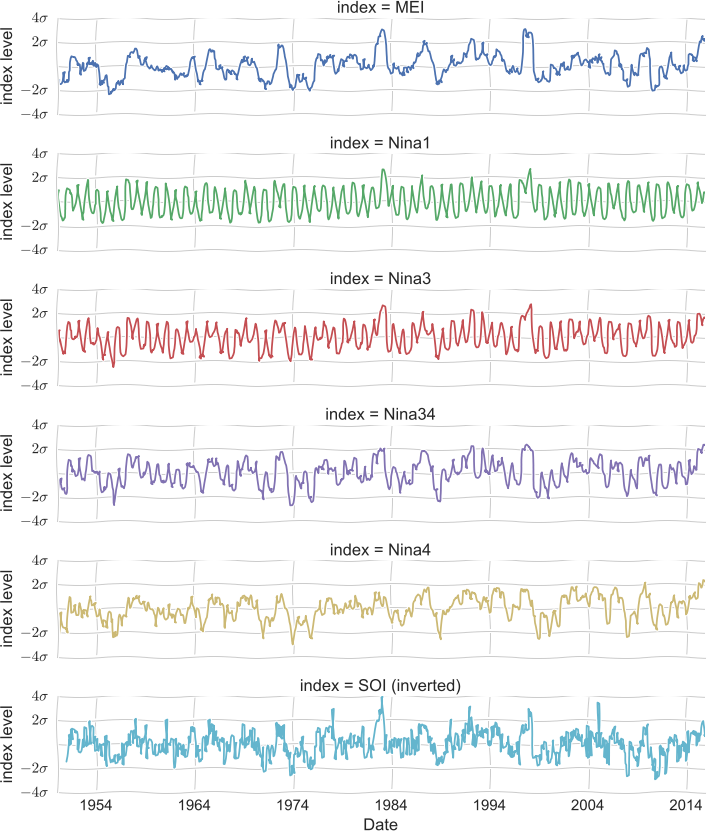
Fig. 2 Chronologies of various ENSO indices. [To see the details of, or to obtain and modify, the analysis presented here, view the ipython notebook source that was used to generate the original figure.]

Okay, so there are ways to document the degree of El Niño or La Niña that is being experienced, what does this imply is happening? Well, changing surface conditions (sea surface temperatures) alter circulation in the atmosphere. Near the equator this shifts the locations most favorable for large scale convection (the rising of warm moist air to produce rainfall) [3 4]. So affected regions will see notably higher or lower rainfall amounts than would be expected under other conditions. Effects are also felt elsewhere as shifts in strength and location of temperature gradients modify the variability of higher latitude circulation, and as conditions in other parts of the globe create their own responses and feedbacks. Results can be very direct, such as low fishing yields in Peru as a result of a lack of high nutrient deep water, to complex shifts from low to high rainfall in West Africa as a result of the length of time it takes local ocean temperatures to adjust to quickly spreading upper air temperature anomalies (Parhi 2016).



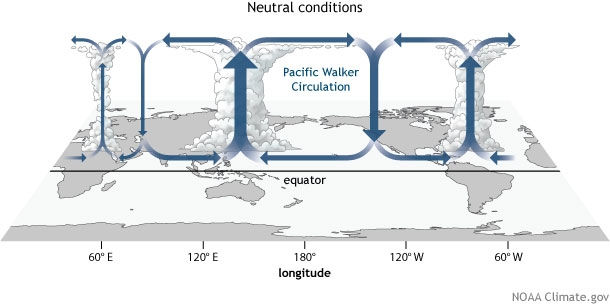
Fig. 3  Diagram of equatorial zonal circulation, as discussed here.


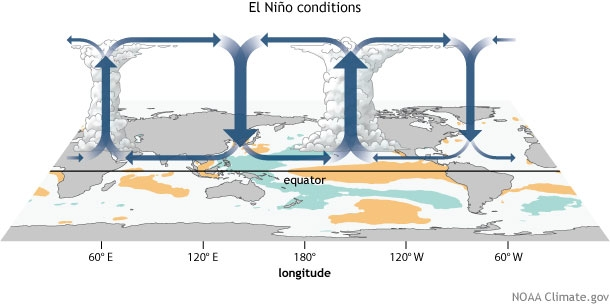
Fig. 4  Diagram of equatorial zonal circulation under El Niño conditions, as discussed here.

 

Yes, and...

So, a large scale redistribution of temperature causes shifts in the location of some major processes, and triggers complex response mechanisms that interact with local environments, to create conditions that would not commonly be observed in that area otherwise. And since the whole thing is tied up in the butterfly effect these conditions are neither perfectly reproducible, nor predictable, nor even fully comprehensible. Thanks Dr. Ian Malcolm, it’s much clearer now. But how do you pull a sense of what to expect from an El Niño out of all this? As said, there is an understanding of relevant mechanisms which, given certain conditions, generally function in discernible ways. But in practice much of the conception of a typical El Niño is based on historical observation (Dilley 2000). ”What was it like the last time? What is it typically like?”


Classification

The first step is to determine when was ”last time”? The historical indices [2] shown earlier can be used to determine this. For the example here we’re going to use the Multivariate ENSO Index (MEI) and consider El Niño events to be those where the index is above the 1σ1σ level. These are common choices, but it’s important to remember that it is still a subjective definition. The periods designated [5] will determine what data we consider for the rest of the example. Not only the estimates that we will create, but also the estimates of the uncertainty of those estimates, must all be given the caveat ”given our definition of an El Niño event”. This is not necessarily a bad thing. For many regions there are very sensible reasons to consider one ENSO indicator as more informative than another, or where there may not be much difference between them. But it’s something to keep in mind

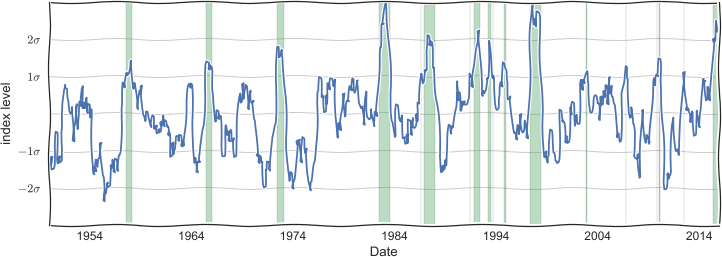
Fig. 5 Time line for ENSO strength as described by the MEI. Shaded bands are considered El Niño periods. [source]


What is happening within the selected periods, and is it different from what might be expected? Let’s consider the general region of Southern Africa [6].

 

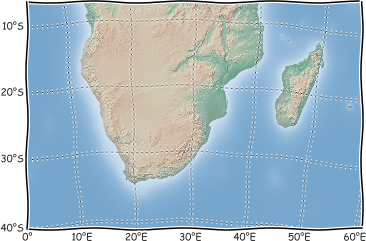
Fig. 6 Chart showing the Southern African region considered in this example. [source]

 

For this example lets look at mean monthly rainfall rates over the region. These values are a very ’broad strokes’ descriptor, and many people have pointed out that such measurements are not the best indicator of the more nuanced variations and chronologies that can directly affect agricultural yields (Tadross 2009) (Ambrosino 2013) or the risk of floods/droughts. It’s been argued that for Southern Africa, increased temperatures are more consistently observed during El Niño events than changes in precipitation patterns, and that droughts are more a result of the interactions between high temperatures and preexisting conditions, than low rainfall alone (Meque 2014). However, often the records needed for more involved studies are not available, and so large scale precipitation estimates are commonly what are reported and extrapolated from. As such, it’s important to have some sense of these products. Here we will consider the Global Precipitation Climatology Project GPCPdata set. As with the selected ENSO index, this is just one option of many. Working with multiple data sources is a complex problem, and will be addressed another time. There’s enough difficulty in reading the message of a single data source to keep us busy right now. Again though, it’s something to keep in mind; every part of the following analysis must be considered to be conditional on the choice of data set (the same as when choosing the El Niño definition).

So, lets look at a few sample months that were selected as occurring within El Niño periods. How are the estimated rainfall values different from what is typically observed on that given month [7]?


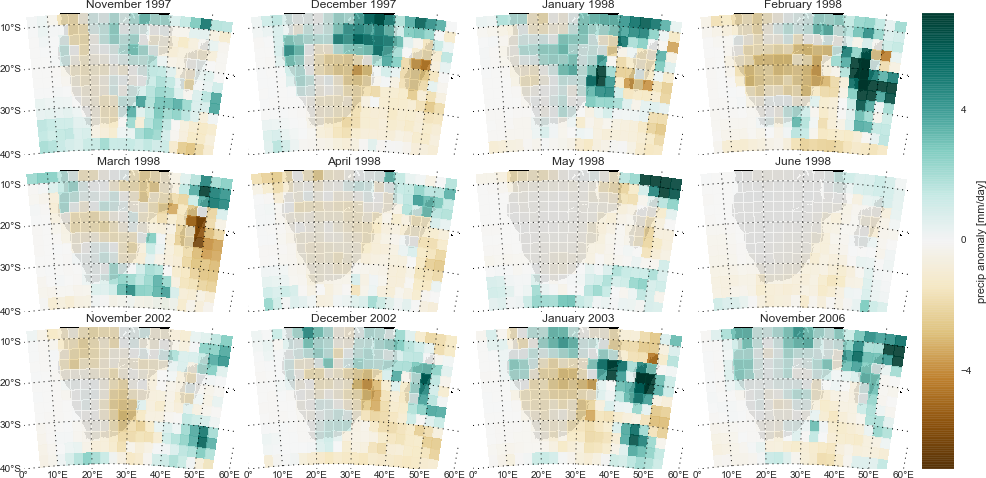
 Fig. 7 Anomalies in mean monthly precipitation rate for selected months within El Niño periods. [source]
Can see that there’s a lot of variation in the patterns. Looking at the cycle of events from November of 1997 to June 1998 suggests that effects were stronger in the austral summer. That is typically the case (Crétat 2010), and also the season when ENSO activity in the Pacific tends to be strongest. Looking at the summer months you can squint, and suggest that there are some common themes, but even they are not fully consistent within the small sample.

The scale of the anomalies also varies. This is expected as rainfall amounts themselves vary between regions and seasons. One of the reasons for selecting the GPCP product for this example is that this group provides error estimates for its monthly estimates. While they state that the procedure for deriving these values is simplistic (Huffman 2009), these estimates are still very useful for suggesting which anomalies are beyond the margin of error for the calculated value. What does the figure above [7] look like when we only consider anomalies that are strongly positive or negative enough to be beyond the estimated measurement error? This does filter out some noise in favor of the major events, although the images themselves are more complicated [8].


 

Fig. 8 Anomalies in mean monthly precipitation rate for selected months within El Niño periods, blanking out anomalies whose magnitude is low enough that they are within the estimated margin of error for the analysis. [source]

Composites

Okay, okay, so measurement and other estimation uncertainties mean that not every detail is significant, and there will always be variation between events. That’s fine, point taken, but what about the big picture? Overall, how do the circulation shifts mentioned earlier on [4] map onto the region?

This is where the composites finally come in. The idea is to make some type of estimate of the central tendencies of the grouped events, to find some way condense the information and filter out the noise of the individual variability1.

The procedure is to first take all the time slices identified as being in El Niño periods, so those shown previously [7] plus sixty-three others, and then calculate the arithmetic mean value for each grid cell. Or the median value, or the mode2. All of which give subtly different information about the data being analyzed, and so create different maps [9].


Fig. 9 Composites of monthly mean precipitation anomalies for El Niǹo periods, created using three different statistics. Note that the ”mode” was estimated by first binning values. [source]

Can see that the the different statistics show different information [9], or maybe could be said to give different impressions. Taking the second perspective they could even be said to contradict each other in places. The mean values will be more modified by extremes1. The mode is determined by a plurality and so ignores other possibilities, even if the value it displays happens only a small fraction of the time. The median takes the most central position, but like the mean is determined from the totality of values and may not represent what could actually occur at any given sample.

What about earlier when we blanked out values that were below a suggested error threshold [8]? How do those values affect the composite statistics? What happens if we do the same calculations but ignore any anomalies that we suspected of being unreliable?

 
 

Fig. 10 Same calculations as in Figure 9, but ignoring anomalies that were below the suggested error threshold. [source]

Ignoring questionable values does produce some interesting shifts in the images. Note that the scale is now [10] three times larger for than it was previously [9]. The mean estimate stays pretty similar, since the low magnitude noise that we are now ignoring would be mostly averaged out when creating the original composite [9]. There are bigger shifts in the median and mode as the low magnitude ’suspect’ values no longer define the mid-point or high frequency values, respectively. However, it becomes much more difficult to interpret these results since the number of samples used for each grid cell is now inconsistent. If all the samples for a particular area where below the error threshold, except for one… then that value becomes the mode of the data. Is that value then really indicative of a consistent El Niño effect? We see that if rather than ignoring questionable values we instead set them to zero [11], the results suggest a more restrictive version of the initial estimate [9].


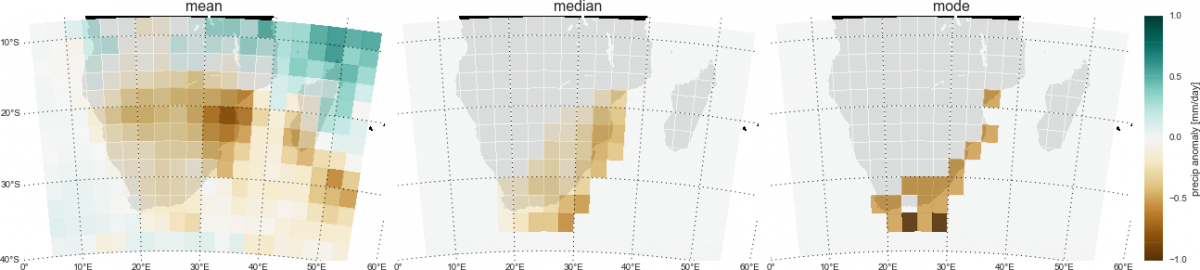
Fig. 11 Same calculations as in Figure 9, but with anomalies that were below the suggested error threshold set to zero. [source]
 

Significance

So why is the number of samples used to do the calculation such a concern? It comes down to the idea of statistical significance; the question of how confident we can be that the associations we observe are not coincidental. If you have a sour stomach after a glass of milk, can you be sure the milk was off, or rather have you just discovered that you’re lactose intolerant? If you smoke five cigarettes with no notable ill effects, does that prove that they’re harmless to you?

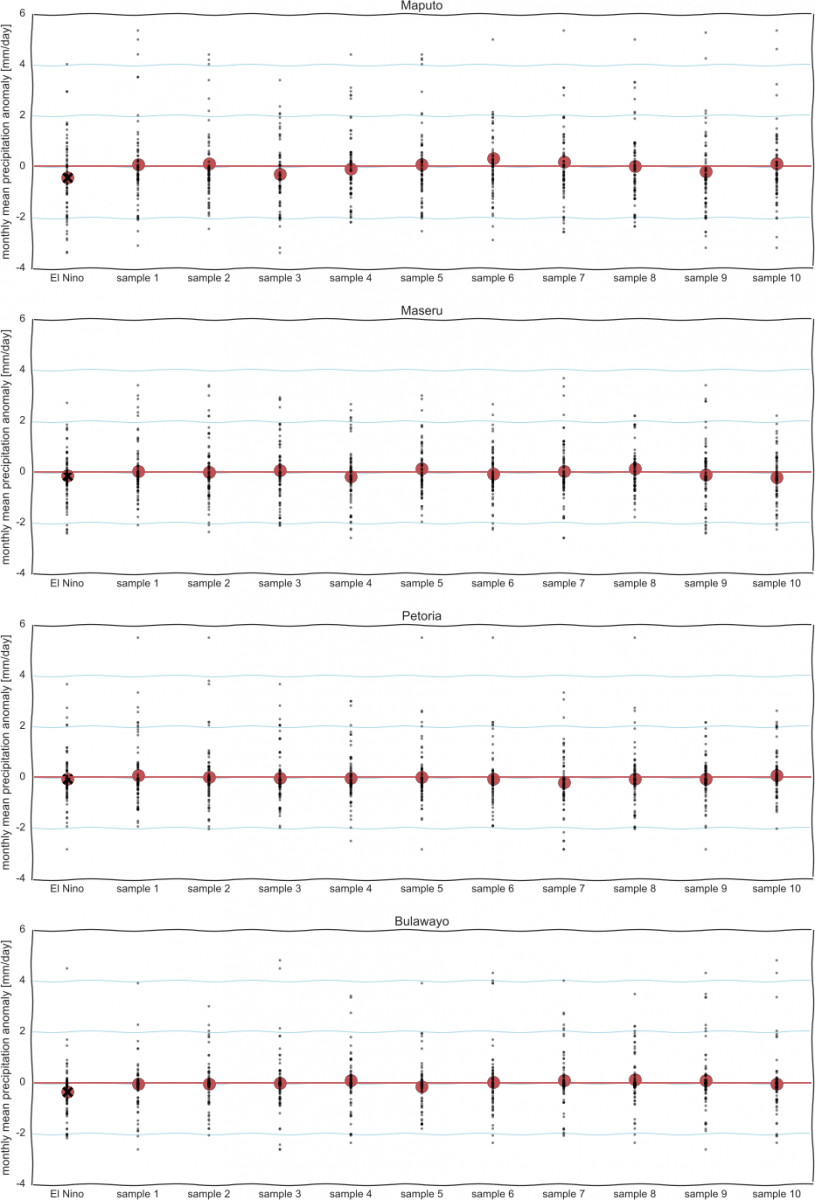
We saw [11] that certain regions see, on average, less rainfall during El Niño periods. But what if we had just pulled the values of a few random months from the full data set and averaged those? Even though the mean anomaly of the full data set is, by definition, zero, the odds are reasonable that you could by chance select only high or low values. Although, the odds of this decrease as the size of the samples increase. To illustrate we’ll consider just four grid cells, which contain large cities in south-east Africa.

  

Fig. 12 The anomaly values for each identified El Niño month are plotted next to ten random samples from the full data set, each containing the same number of elements (75) as the El Niño sample. The means of each of these samples is plotted as a red circle, with an ’X’ emphasizing the mean of the El Niño sample. The zero level is highlighted with a red line. [source]

 

These examples [12] show that there are a wide range of observed values, even for the El Niño sample. All the El Niño samples have an average value subtly below zero. However, does this indicate that El Niño periods are more likely to have lower than average rainfall in all these regions, or is the difference in line with the variation in the mean values that we see produced by the random samples?

Ten random samples isn’t enough to give a clear idea, so we consider this procedure for a thousand such samples.

 

Fig. 13 Mean value of the El Niño samples (marked with an ’X’), plotted along with the mean value of 1000 other samples, all of the same size (75) as the El Niño sample. The zero level is emphasized with a red line. The blue shaded area shows the range that 95%95% of the randomly generated means fall under. [source]

We see [13] that for Maputo and Bulawayo the mean El Niño value is low enough that it appears that it is unlikely, although clearly not impossible, for it to be generated by selecting seventy-five random elements. The values for Maseru and Petoria, however, fall within the range of values easily obtained by sampling at random. Even though both have on average negative anomalies during identified El Niño periods, this analysis suggests that it is less likely that these associations are not coincidental, or perhaps rather that El Niño is not a singular dominant driver for variation in those regions.

So how does considering the significance of the statistics affect our composite images [9]? What is the result if we perform the same test [13] for each grid cell and block out those that don’t pass?


Fig. 14 Composite mean of El Niño events. Values with magnitudes determined to be less than 95%95% significant and blocked out in gray. [source]

The graphic [14] here is created only for the composite mean this time. The other values are just as potentially informative, but as the mean is the most commonly reported and requested statistic, it seems worth concentrating on it for the moment1. Blocking out ’insignificant’ values [14] doesn’t drastically change the impression we had before [9]. However it does emphasize some of the nuances in the calculation.

It’s important to note that the significance testing method used here is rejection based. That is, we first select a threshold, in this case a commonly used, but arbitrary, one. Then mean anomalies that aren’t large enough in magnitude, that is aren’t adequately strongly positive or negative, are rejected. This let’s us determine where we have reason to be confident that there is an association between El Niño and rainfall. However, the approach doesn’t distinguish between areas where we could be confident that there isn’t an association and those where there just isn’t enough data to tell. It also doesn’t say how confident we are in the particular value that has been selected to represent the association. To make those statements would require a different approach.

 

Some comments

So, what have we ended up with? The goal here wasn’t to state what an El Niño is and what it does, but rather to deconstruct where some of the general ideas about El Niño come from. Hopefully we made some steps in that direction.

It’s important to remember that the analysis shown here is just looking at how one, not necessarily all that relevant, variable (average monthly rainfall), associates with one particular indicator of El Niño behavior (MEI), in one particular interpretation of observational records (GPCP). Change any of these baseline factors and the images shown above will change accordingly.

Even within a defined dataset there are many different features to consider, which reveal different attributes. We’ve seen that areas which have strong overall response signals can show considerable variability even within El Niño periods [7 12]. For example, sometimes warm ocean temperatures in the Indian Ocean create offshore cyclones that pull moisture away from Mozambique, other times these cyclones make land fall and create floods (Mason 1997).

Understanding of how El Niño events can affect Southern Africa is becoming more nuanced, such as how temperature gradients across the Indian and Southern Oceans modulate local responses (Malherbe 2014). These advances, and an increase in observational data, can allow for the identification of more refined patterns, and hopefully allow forecasts to more subtly account for conditions. These developments, however, won’t remove the multiplicity of data sources and analysis methods. What is noise, and what is signal, is subjective and context based, and dependent on the spatial scale and time frame addressed by an inquiry. Looking at a multitude of different figures and interpretations often leads people to ask ”well, which one’s right?”. Here, if you trust my calculations1, they are all right, just the answers to very specific questions. It’s often lamented that ”computers are difficult to work with, not because they don’t do what you tell them, but because they do exactly what you tell them.” The same is true with maths. Often the most difficult part of science isn’t obtaining results, it’s figuring out what we’re really asking and to what extent the data at hand can relate to it.

 

References

  1. Andrew Hoell, Chris Funk, Tamuka Magadzire, Jens Zinke, Greg Husak. El NiñoSouthern Oscillation diversity and Southern Africa teleconnections during Austral Summer. Clim Dyn 45, 1583–1599 (2014). Link

  2. Pradipta Parhi, Alessandra Giannini, Pierre Gentine, Upmanu Lall. Resolving Contrasting Regional Rainfall Responses to El Niño over Tropical Africa. Journal of Climate 29, 1461–1476 (2016). Link

  3. Maxx Dilley. Reducing Vulnerability to Climate Variability in Southern Africa: The Growing Role of Climate Information. 63–73 (2000). Link

  4. M Tadross, P Suarez, A Lotsch, S Hachigonta, M Mdoka, L Unganai, F Lucio, D Kamdonyo, M Muchinda. Growing-season rainfall and scenarios of future change in southeast Africa: implications for cultivating maize. Climate Research 40, 147–161 (2009). Link

  5. Chiara Ambrosino, Richard E. Chandler, Martin C. Todd. Rainfall-derived growing season characteristics for agricultural impact assessments in South Africa. Theoretical and Applied Climatology 115, 411–426 (2013). Link

  6. Arlindo Meque, Babatunde J. Abiodun. Simulating the link between ENSO and summer drought in Southern Africa using regional climate models. Clim Dyn 44, 1881–1900 (2014).Link

  7. Julien Crétat, Yves Richard, Benjamin Pohl, Mathieu Rouault, Chris Reason, Nicolas Fauchereau. Recurrent daily rainfall patterns over South Africa and associated dynamics during the core of the austral summer. International Journal of Climatology 32, 261–273 (2010). Link

  8. George J. Huffman, Robert F. Adler, David T. Bolvin, Guojun Gu. Improving the global precipitation record: GPCP Version 2.1. Geophys. Res. Lett. 36 (2009). Link

  9. S.J. Mason, M.R. Jury. Climatic variability and change over southern Africa: a reflection on underlying processes. Progress in Physical Geography 21, 23–50 (1997). Link

  10. Johan Malherbe, Willem A. Landman, Francois A. Engelbrecht. The bi-decadal rainfall cycle Southern Annular Mode and tropical cyclones over the Limpopo River Basin, southern Africa. Clim Dyn 42, 3121–3138 (2014). Link

 
 
Disclaimer: The views expressed here are solely those of the author in her private capacity and do not in any way represent the views of the ACDI, or any other entity affiliated with the ACDI.